Materi Matematika Pecahan Memahami Konsep dan Penerapannya

Berita Terkait

Materi matematika pecahan merupakan fondasi penting dalam memahami berbagai konsep matematika lainnya. Dari pembagian kue hingga perhitungan persentase, pecahan selalu hadir dalam kehidupan sehari-hari. Materi ini akan membahas secara menyeluruh tentang pecahan, mulai dari definisi, konsep dasar, operasi, penyederhanaan, pecahan senilai, hingga penerapannya dalam kehidupan nyata.

Materi ini akan menguraikan definisi pecahan, perbedaan pecahan biasa, campuran, dan desimal. Lebih lanjut, kita akan mengkaji konsep pembilang dan penyebut, serta berbagai operasi matematika yang melibatkan pecahan, seperti penjumlahan, pengurangan, perkalian, dan pembagian. Metode penyederhanaan pecahan dan penentuan pecahan senilai juga akan dijelaskan secara rinci. Selain itu, kita akan melihat contoh-contoh nyata penerapan pecahan dalam kehidupan sehari-hari, seperti membagi kue atau menghitung diskon.

Definisi Materi Pecahan

Pecahan dalam matematika merupakan bagian dari suatu keseluruhan. Pemahaman tentang pecahan sangat penting untuk berbagai aplikasi matematika, mulai dari perhitungan sederhana hingga konsep yang lebih kompleks.

Bentuk-Bentuk Pecahan

Pecahan dapat dibedakan menjadi beberapa bentuk, masing-masing memiliki karakteristik tersendiri. Memahami perbedaan ini sangat membantu dalam melakukan operasi matematika dengan pecahan.

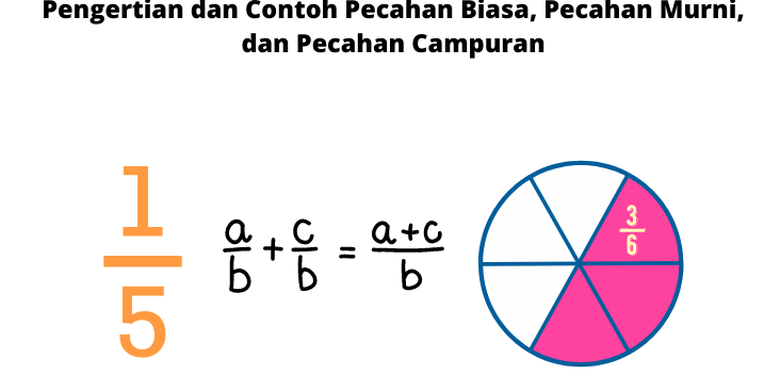
Pecahan Biasa: Pecahan biasa terdiri dari pembilang dan penyebut. Pembilang menunjukkan jumlah bagian yang diambil, sedangkan penyebut menunjukkan jumlah bagian keseluruhan. Contoh: ³/ ₄ (dibaca tiga per empat).
Pecahan Campuran: Pecahan campuran merupakan gabungan antara bilangan bulat dan pecahan biasa. Contoh: 1 ²/ ₃ (dibaca satu dua per tiga).
Pecahan Desimal: Pecahan desimal menggunakan titik desimal untuk menunjukkan nilai pecahan. Contoh: 0,75 (dibaca nol koma tujuh lima).

Perbandingan Bentuk-Bentuk Pecahan

Berikut tabel yang membandingkan ketiga bentuk pecahan tersebut:

Bentuk Pecahan	Definisi	Contoh
Pecahan Biasa	Terdiri dari pembilang dan penyebut.	¹/₂, ³/₄, ⁵/₈
Pecahan Campuran	Gabungan bilangan bulat dan pecahan biasa.	1¹/₂, 2³/₅, 3²/₇
Pecahan Desimal	Menggunakan titik desimal untuk menunjukkan nilai pecahan.	0,5, 0,75, 1,25

Hubungan Antar Bentuk Pecahan

Ketiga bentuk pecahan ini saling terkait dan dapat dikonversi satu sama lain. Konversi antara pecahan biasa, pecahan campuran, dan pecahan desimal merupakan keterampilan penting dalam matematika.

Konsep Dasar Pecahan

Pecahan merupakan bagian dari keseluruhan. Pemahaman tentang pembilang dan penyebut menjadi kunci untuk memahami nilai pecahan. Memahami konsep ini akan membantu dalam berbagai operasi matematika selanjutnya.

Penjelasan Pembilang dan Penyebut

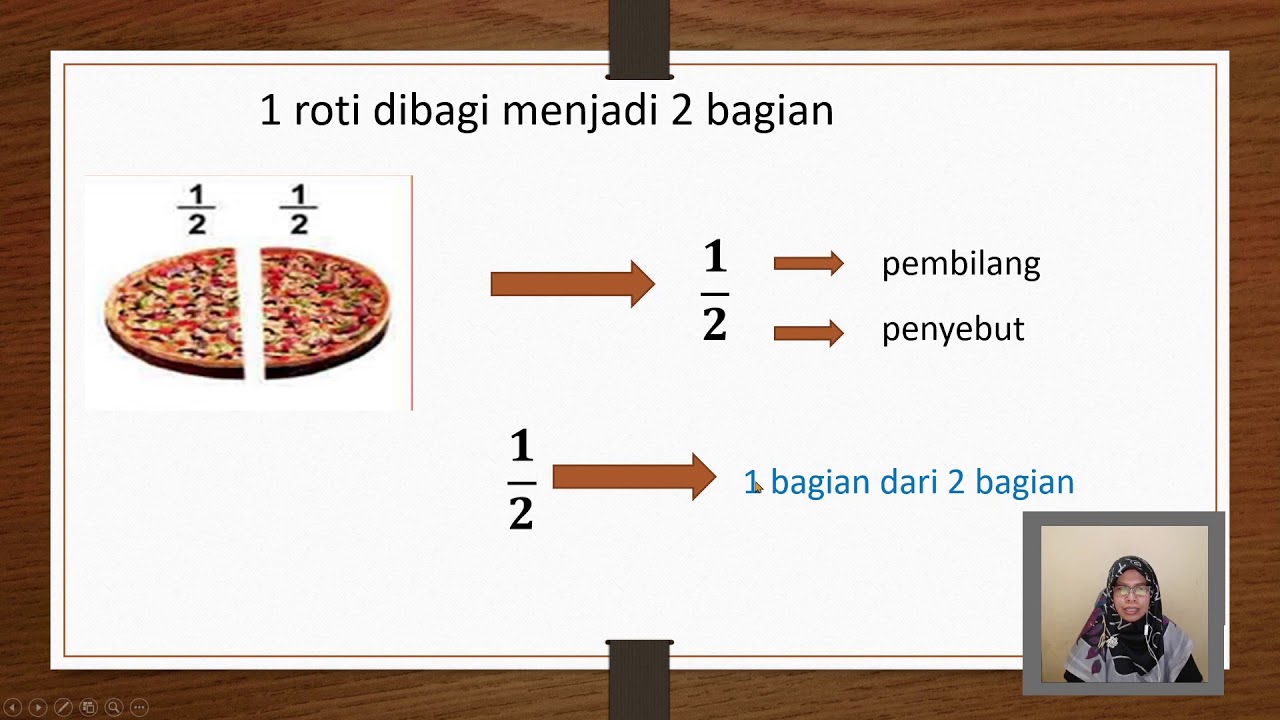
Dalam sebuah pecahan, bagian atas disebut pembilang dan bagian bawah disebut penyebut. Pembilang menunjukkan jumlah bagian yang dipertimbangkan, sedangkan penyebut menunjukkan jumlah keseluruhan bagian yang sama besar.

Contoh Penggunaan Pembilang dan Penyebut

Bayangkan sebuah pizza yang dipotong menjadi 8 bagian sama besar. Jika Anda mengambil 3 potong, maka 3 adalah pembilang dan 8 adalah penyebut, yang ditulis sebagai 3/8. Ini menunjukkan bahwa Anda memiliki 3 bagian dari 8 bagian pizza yang tersedia.

Contoh lain, jika terdapat 10 kelereng dan 4 diantaranya berwarna merah, maka pecahannya adalah 4/10. 4 adalah pembilang (jumlah kelereng merah) dan 10 adalah penyebut (jumlah total kelereng).

Langkah-Langkah Memahami Nilai Pecahan

Identifikasi pembilang dan penyebut dalam pecahan.
Pahami bahwa penyebut menunjukkan jumlah bagian yang sama besar dalam keseluruhan.
Pembilang menunjukkan jumlah bagian yang sedang dipertimbangkan.
Hubungkan pembilang dan penyebut untuk memahami bagian dari keseluruhan.
Contoh: Dalam pecahan 5/7, penyebut 7 menunjukkan bahwa keseluruhan dibagi menjadi 7 bagian yang sama besar, dan pembilang 5 menunjukkan bahwa kita mempertimbangkan 5 bagian dari keseluruhan tersebut.

Operasi pada Pecahan

Memahami operasi pada pecahan sangat penting dalam matematika. Kemampuan ini akan memudahkan kita dalam menyelesaikan berbagai permasalahan yang melibatkan pecahan, baik dalam kehidupan sehari-hari maupun dalam konteks akademis.

Penjumlahan Pecahan

Penjumlahan pecahan dapat dilakukan dengan beberapa cara, tergantung pada penyebutnya. Jika penyebutnya sama, kita cukup menjumlahkan pembilangnya dan penyebutnya tetap sama. Jika penyebutnya berbeda, kita perlu menyamakan penyebutnya terlebih dahulu dengan mencari KPK (Kelipatan Persekutuan Terkecil).

Pecahan dengan penyebut sama: a/c + b/c = (a+b)/c
Pecahan dengan penyebut berbeda: a/b + c/d = (ad+bc)/bd

Contoh:

1/4 + 2/4 = (1+2)/4 = 3/4

1/2 + 1/3 = (1×3 + 1×2) / (2×3) = 5/6

Ilustrasi visual: Bayangkan sebuah pizza dibagi menjadi 4 bagian. Jika kita mengambil 1 bagian dan kemudian 2 bagian lagi, total yang kita miliki adalah 3 bagian dari 4 bagian.

Pengurangan Pecahan

Pengurangan pecahan mirip dengan penjumlahan. Jika penyebutnya sama, kita kurangi pembilangnya dan penyebutnya tetap sama. Jika penyebutnya berbeda, kita perlu menyamakan penyebutnya.

Pecahan dengan penyebut sama: a/c – b/c = (a-b)/c
Pecahan dengan penyebut berbeda: a/b – c/d = (ad-bc)/bd

Contoh:

3/5 – 1/5 = (3-1)/5 = 2/5

2/3 – 1/4 = (2×4 – 1×3) / (3×4) = 5/12

Ilustrasi visual: Bayangkan sebuah kue dibagi menjadi 5 bagian. Jika kita mengambil 3 bagian dan kemudian memberikan 1 bagian, maka yang tersisa adalah 2 bagian dari 5 bagian.

Perkalian Pecahan, Materi matematika pecahan

a/b x c/d = (a x c) / (b x d)

Perkalian pecahan dilakukan dengan mengalikan pembilang dengan pembilang dan penyebut dengan penyebut.

Contoh:

2/3 x 1/2 = (2 x 1) / (3 x 2) = 2/6 = 1/3

Ilustrasi visual: Bayangkan sebuah kotak dibagi menjadi 3 bagian. Jika kita mengambil 2 bagian dari 3 bagian dan kemudian mengambil separuh dari 2 bagian tersebut, maka kita memiliki 1 bagian dari 3 bagian.

Pembagian Pecahan

a/b ÷ c/d = (a/b) x (d/c)

Pembagian pecahan dilakukan dengan mengalikan pecahan pertama dengan kebalikan (reciprocal) dari pecahan kedua.

Contoh:

3/4 ÷ 1/2 = (3/4) x (2/1) = 6/4 = 3/2

Ilustrasi visual: Bayangkan sebuah batang dibagi menjadi 4 bagian. Jika kita mengambil 3 bagian dan membaginya menjadi 2 bagian sama besar, maka masing-masing bagian akan berukuran 3/2 bagian dari ukuran keseluruhan.

Menyederhanakan Pecahan

Menyederhanakan pecahan adalah proses mengubah pecahan menjadi bentuk yang paling sederhana tanpa mengubah nilainya. Teknik ini penting untuk mempermudah perhitungan dan pemahaman konsep pecahan.

Metode Menyederhanakan Pecahan

Ada beberapa metode untuk menyederhanakan pecahan. Metode yang paling umum adalah dengan membagi pembilang dan penyebut dengan faktor persekutuan terbesar (FPB).

Pembagian Berulang: Metode ini melibatkan pembagian berulang pembilang dan penyebut dengan faktor persekutuan sampai tidak ada lagi faktor persekutuan yang dapat dibagi.
Faktorisasi Prima: Metode ini melibatkan pencarian faktorisasi prima dari pembilang dan penyebut. FPB dapat ditemukan dengan mengalikan faktor prima yang sama dari pembilang dan penyebut.

Contoh Kasus Menyederhanakan Pecahan

Berikut beberapa contoh kasus penyederhanaan pecahan dengan cara yang berbeda:

Contoh 1 (Pembagian Berulang): Untuk menyederhanakan pecahan ¹²⁄ ₁₈, kita dapat membagi pembilang dan penyebut dengan faktor persekutuan 2. Hasilnya adalah ⁶⁄ ₉. Kita dapat membagi lagi dengan 3, menghasilkan ²⁄ ₃. Pecahan ²⁄ ₃ sudah dalam bentuk paling sederhana.
Contoh 2 (Faktorisasi Prima): Untuk menyederhanakan pecahan ¹⁵⁄ ₂₅, kita cari faktorisasi prima dari 15 (3 × 5) dan 25 (5 × 5). FPB dari 15 dan 25 adalah 5. Kemudian, bagi pembilang dan penyebut dengan 5. Hasilnya adalah ³⁄ ₅.
Contoh 3 (Kasus Kompleks): Misalnya pecahan ⁴²⁄ ₅₆. Dengan pembagian berulang, kita bisa membagi dengan 2, lalu 2 lagi, dan akhirnya 7. Proses ini menghasilkan pecahan sederhana ³⁄ ₄.

Faktor Persekutuan Terbesar (FPB)

Faktor persekutuan terbesar (FPB) adalah faktor terbesar yang dapat membagi habis dua atau lebih bilangan bulat secara bersamaan. FPB sangat penting dalam menyederhanakan pecahan karena membantu menemukan bentuk paling sederhana dari suatu pecahan tanpa mengubah nilai sebenarnya.

Berikut cara menemukan FPB:

Daftar faktor: Buat daftar faktor dari masing-masing bilangan.
Faktor persekutuan: Temukan faktor-faktor yang sama pada kedua daftar.
Faktor terbesar: Faktor terbesar dari faktor-faktor persekutuan tersebut adalah FPB.

Sebagai contoh, untuk menemukan FPB dari 12 dan 18, kita bisa mencari faktor-faktor dari 12 (1, 2, 3, 4, 6, 12) dan faktor-faktor dari 18 (1, 2, 3, 6, 9, 18). Faktor persekutuannya adalah 1, 2, 3, dan 6. FPB-nya adalah 6.

Pecahan Senilai

Pecahan senilai adalah pecahan-pecahan yang memiliki nilai yang sama meskipun penulisannya berbeda. Memahami pecahan senilai penting untuk berbagai operasi aritmatika dengan pecahan, seperti penjumlahan, pengurangan, dan perbandingan.

Definisi Pecahan Senilai

Pecahan senilai adalah pecahan-pecahan yang merepresentasikan bagian yang sama dari keseluruhan. Meskipun penulisannya berbeda, nilai yang diwakilinya tetap sama.

Cara Menemukan Pecahan Senilai

Pecahan senilai dapat ditemukan dengan mengalikan atau membagi pembilang dan penyebut pecahan awal dengan angka yang sama. Ini tidak mengubah nilai pecahan, karena sama seperti mengalikan atau membagi dengan angka 1.

Perkalian: Jika pembilang dan penyebut dikalikan dengan angka yang sama, pecahan yang dihasilkan senilai dengan pecahan awal. Contoh: (1/2) dikalikan dengan (2/2) menghasilkan (2/4), yang senilai dengan 1/2.
Pembagian: Jika pembilang dan penyebut dibagi dengan angka yang sama, pecahan yang dihasilkan senilai dengan pecahan awal. Contoh: (4/8) dibagi dengan (4/4) menghasilkan (1/2), yang senilai dengan 4/8.

Contoh Pecahan Senilai

Pecahan Awal	Pecahan Senilai (dikalikan 2)	Pecahan Senilai (dikalikan 3)	Pecahan Senilai (dibagi 2)
1/2	2/4	3/6	(tidak berlaku, karena pembilang kurang dari penyebut setelah dibagi 2)
2/3	4/6	6/9	(tidak berlaku, karena pembilang kurang dari penyebut setelah dibagi 2)
3/4	6/8	9/12	(tidak berlaku, karena pembilang kurang dari penyebut setelah dibagi 2)
5/6	10/12	15/18	(tidak berlaku, karena pembilang kurang dari penyebut setelah dibagi 2)

Tabel di atas menunjukkan beberapa contoh pecahan senilai yang diperoleh dengan mengalikan atau membagi pembilang dan penyebut pecahan awal dengan angka yang sama. Perhatikan bahwa pembagian hanya berlaku jika hasil pembagian pembilang dan penyebut adalah bilangan bulat.

Pecahan Campuran dan Desimal

Memahami hubungan antara pecahan biasa, pecahan campuran, dan desimal sangat penting dalam matematika. Ketiga bentuk ini merupakan representasi berbeda dari nilai yang sama. Kemampuan untuk mengubah di antara bentuk-bentuk ini sangat membantu dalam menyelesaikan berbagai soal matematika.

Mengubah Pecahan Biasa Menjadi Pecahan Campuran

Pecahan biasa yang bernilai lebih dari 1 dapat diubah menjadi pecahan campuran. Proses ini melibatkan pembagian pembilang dengan penyebut. Hasil bagi merupakan bilangan bulat pada pecahan campuran, sedangkan sisa pembagian menjadi pembilang pada pecahan. Penyebut tetap sama.

Contoh: Ubah pecahan biasa 5/2 menjadi pecahan campuran. 5 dibagi 2 menghasilkan 2 sisa 1. Jadi, pecahan campurannya adalah 2 1/2.

Mengubah Pecahan Campuran Menjadi Pecahan Biasa

Untuk mengubah pecahan campuran menjadi pecahan biasa, kalikan bilangan bulat dengan penyebut, kemudian tambahkan hasil perkalian dengan pembilang. Hasil penjumlahan tersebut menjadi pembilang baru, dan penyebutnya tetap sama.

Contoh: Ubah pecahan campuran 3 2/5 menjadi pecahan biasa. (3 x 5) + 2 = 17. Jadi, pecahan biasanya adalah 17/5.

Mengubah Pecahan Campuran Menjadi Desimal

Untuk mengubah pecahan campuran menjadi desimal, ubah terlebih dahulu pecahan campuran menjadi pecahan biasa. Kemudian, bagi pembilang dengan penyebut untuk mendapatkan nilai desimal.

Contoh: Ubah pecahan campuran 1 3/4 menjadi desimal. Pecahan biasa dari 1 3/4 adalah 7/4. 7 dibagi 4 adalah 1,75. Jadi, desimalnya adalah 1,75.

Mengubah Pecahan Biasa Menjadi Desimal

Untuk mengubah pecahan biasa menjadi desimal, bagi pembilang dengan penyebut. Hasil bagi merupakan nilai desimal.

Contoh: Ubah pecahan biasa 3/8 menjadi desimal. 3 dibagi 8 adalah 0,375. Jadi, desimalnya adalah 0,375.

Mengubah Desimal Menjadi Pecahan Biasa

Untuk mengubah desimal menjadi pecahan biasa, tuliskan desimal sebagai pecahan dengan penyebut 10, 100, 1000, dan seterusnya, tergantung pada jumlah tempat desimal. Kemudian sederhanakan pecahan tersebut.

Contoh: Ubah desimal 0,75 menjadi pecahan biasa. Tulis sebagai 75/100. Kemudian sederhanakan menjadi 3/4.

Penerapan Materi Pecahan dalam Kehidupan Sehari-hari

Pemahaman tentang pecahan tak hanya penting dalam dunia matematika, tetapi juga sangat berguna dalam kehidupan sehari-hari. Dari membagi kue hingga menghitung diskon, pecahan berperan penting dalam berbagai situasi. Mari kita telusuri beberapa penerapannya.

Contoh Penerapan dalam Membagi Sumber Daya

Penggunaan pecahan sangat umum dalam pembagian sumber daya. Bayangkan Anda memiliki satu kue yang ingin dibagikan kepada beberapa orang. Cara membagi kue secara adil melibatkan konsep pecahan. Misalnya, jika kue dipotong menjadi 8 bagian sama besar, setiap orang akan mendapatkan 1/8 bagian kue.

Penerapan dalam Perhitungan Proporsi

Membuat Resep: Resep masakan seringkali menggunakan pecahan untuk menunjukkan perbandingan bahan-bahan. Misalnya, sebuah resep kue mungkin membutuhkan 2/3 cangkir tepung dan 1/2 cangkir gula. Pemahaman pecahan memungkinkan Anda menyesuaikan resep dengan jumlah yang diinginkan.
Menentukan Persentase: Persentase adalah bentuk lain dari pecahan. Dalam berbagai konteks, seperti menghitung diskon atau presentase kenaikan harga, pemahaman pecahan sangatlah penting.
Menghitung Waktu: Pecahan juga bisa digunakan untuk menghitung waktu. Misalnya, jika Anda membutuhkan waktu 1/2 jam untuk mengerjakan tugas tertentu, Anda dapat mengestimasi berapa lama waktu yang dibutuhkan untuk menyelesaikan beberapa tugas serupa.

Penerapan dalam Pengukuran

Pecahan juga berperan dalam pengukuran. Ketika kita mengukur panjang, lebar, atau volume sesuatu, seringkali kita menggunakan satuan yang terbagi menjadi beberapa bagian. Penggunaan pecahan memungkinkan kita untuk lebih presisi dalam pengukuran.

Penerapan dalam Perhitungan Keuangan

Di bidang keuangan, pecahan digunakan untuk berbagai hal, mulai dari menghitung diskon hingga menentukan suku bunga. Sebagai contoh, jika sebuah barang dijual dengan diskon 25%, maka pecahan 1/4 akan digunakan untuk menghitung besaran diskon tersebut.

Ilustrasi Sederhana: Membagi Kue

Bayangkan Anda memiliki sebuah kue yang ingin dibagikan kepada 4 orang teman. Untuk membagi kue secara adil, Anda perlu memotong kue menjadi 4 bagian yang sama besar. Setiap teman akan mendapatkan 1/4 bagian kue. Ini adalah ilustrasi sederhana tentang penerapan pecahan dalam pembagian.

Latihan Soal dan Pembahasan: Materi Matematika Pecahan

Berikut disajikan beberapa latihan soal pecahan dengan berbagai tingkat kesulitan, lengkap dengan pembahasannya. Latihan ini diharapkan dapat memperkuat pemahaman Anda tentang operasi dan konsep-konsep penting dalam pecahan.

Soal Latihan 1

Hitunglah hasil dari 2/3 + 1/4.

Pembahasan: Untuk menjumlahkan dua pecahan, kita perlu menyamakan penyebutnya terlebih dahulu. Kelipatan persekutuan terkecil (KPK) dari 3 dan 4 adalah
12. Kita ubah kedua pecahan menjadi pecahan senilai dengan penyebut 12:

(2/3) × (4/4) = 8/12

(1/4) × (3/3) = 3/12

Sekarang, jumlahkan kedua pecahan tersebut:

8/12 + 3/12 = 11/12

Jadi, hasil penjumlahan 2/3 + 1/4 adalah 11/12.

Soal Latihan 2

Berapakah hasil dari 5/6 dikurangi 2/9?

Pembahasan: Sama seperti penjumlahan, kita harus menyamakan penyebut terlebih dahulu. KPK dari 6 dan 9 adalah 18.

(5/6) × (3/3) = 15/18

(2/9) × (2/2) = 4/18

Sekarang, kurangi kedua pecahan:

15/18 – 4/18 = 11/18

Jadi, hasil pengurangan 5/6 – 2/9 adalah 11/18.

Soal Latihan 3

Jika 3/5 dari suatu bilangan adalah 12, berapakah bilangan tersebut?

Pembahasan: Jika 3/5 dari suatu bilangan adalah 12, maka kita dapat menulis persamaan: (3/5) × x =
12. Untuk mencari x, kita kalikan kedua ruas dengan invers dari 3/5, yaitu 5/3:

x = 12 × (5/3) = 4 × 5 = 20

Jadi, bilangan tersebut adalah 20.

Soal Latihan 4

Tentukan pecahan senilai dari 2/8 yang penyebutnya 16.

Pembahasan: Untuk mencari pecahan senilai dengan penyebut 16, kita perlu mencari faktor yang dapat digunakan untuk mengalikan penyebut 8 agar menjadi
16. Dalam hal ini, 8 × 2 =
16. Maka, kita kalikan pembilang dan penyebut dengan 2:

(2/8) × (2/2) = 4/16

Jadi, pecahan senilai dari 2/8 dengan penyebut 16 adalah 4/16.

Soal Latihan 5

Seorang peternak memiliki 2 1/2 kg pakan ternak. Jika ia ingin membagikan pakan tersebut kepada 5 ekor sapi secara merata, berapa kg pakan yang diterima setiap sapi?

Pembahasan: Pertama, ubah pecahan campuran menjadi pecahan biasa: 2 1/2 = 5/2 kg. Kemudian, bagi jumlah pakan dengan jumlah sapi: (5/2) ÷ 5 = (5/2) × (1/5) = 1/2 kg.

Jadi, setiap sapi menerima 1/2 kg pakan ternak.

Simpulan Akhir

Setelah mempelajari materi ini, diharapkan pembaca memiliki pemahaman yang komprehensif tentang pecahan. Dari contoh-contoh yang telah dibahas, diharapkan pembaca dapat mengaplikasikan konsep pecahan dalam berbagai situasi kehidupan sehari-hari. Dengan menguasai materi ini, pembaca akan lebih siap menghadapi tantangan matematika yang lebih kompleks di masa depan.